空載狀態工作的變壓器的等效電路及矢量圖示于圖 1-3。
圖中,r1 表示初級繞組直流電阻,Xsl或 Ls1 表示由初級繞組漏磁通產生的漏感抗或漏感 ,rc 為鐵心損耗電阻 ,Xm 或 Lm 表示初級繞組除漏磁通外的自感抗或自感 , 又稱激磁電抗。
空載時,初級繞組的電壓降一般是很小的,所以 U1 和 E1 之值相差很小,故變壓器空載電壓比仍可近似等于其匝數比。即
U1 N1
U2 N2
對于中小功率變壓器來說,由于初級漏感較小,故Xsl或 Ls1可忽略不計, 此時
U1 ≈-E1+I0r1 (1—9)
現在研究變壓器在負載工作時的物理過程。
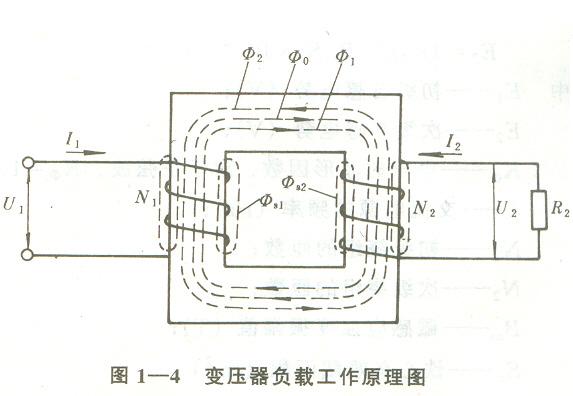
如果在變壓器初級繞組供給電壓U1 , 次級繞組與負載相連 ( 圖 1-4)。這時, 次級繞組將有電流 I2 流過, 在鐵心中產生磁通Φ2 , Φ2的方向應與Φ0方向相反。Φ2 穿過初級繞組后, 初級繞組便從電源取得電流 I1 , 而 I1又產生與Φ2相反的磁通Φ1.。顯然,Φ2 = -Φ1 , 兩個磁通相互抵消 ,結果, 磁路中只剩下一個由空載電流所建立的磁通Φ0。
電流 I1 的數值可依據能量守恒定律求得。如果忽略鐵心和繞組的功率損耗 , 則初級繞組的功率就等 于次級繞組的功率 , 即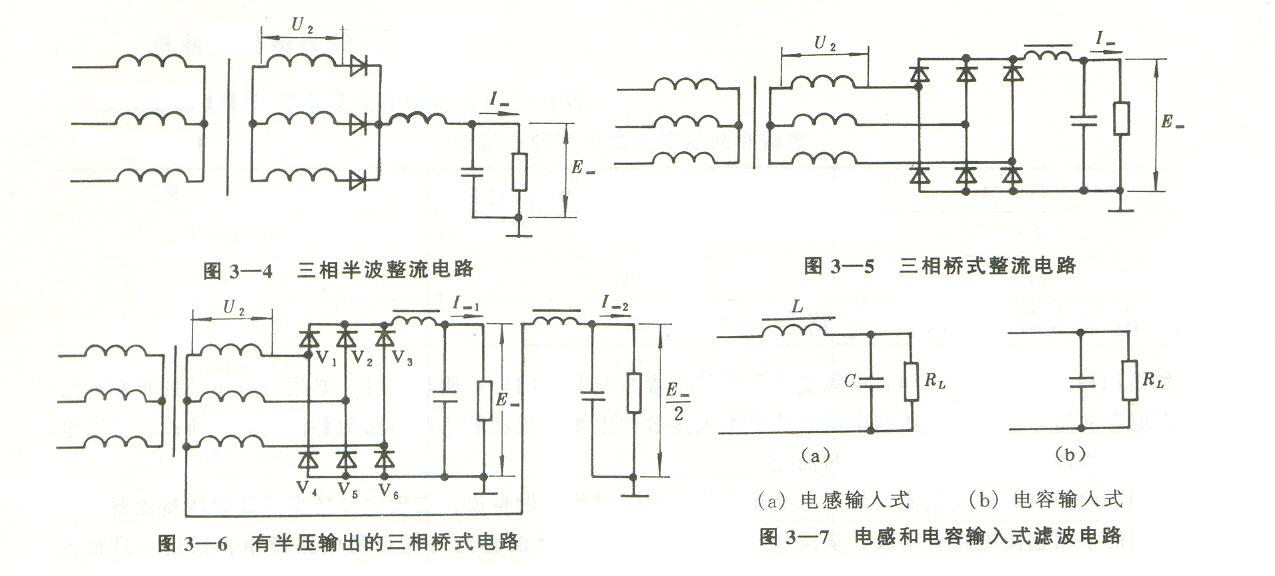 
E1I1 = E2I2 (1—10)
所以
E1 I2
E2 I1 (1—11)
比較式(1—3)和式(1—11) 可得
N1 I2
N2 I1 (1—12)
I2N2
N1 (1—13)
上面已經確定 ,當負載電流的數值不同時,變壓器鐵心中的磁通是不變的。因此 ,建立該磁通的磁勢也是不變的。由此可得
aw0 = awH (1—14)
式中 aw0—空載時的安匝數；
awH—負載時的安匝數。
空載時的安匝數為
aw0 = I0N1 (1—15)
在負載情況下,初、次級繞組安匝數總和為
awH = I1N1+ I2N2 (1—16)
故 I0N1 = I1N1+ I2N2 (1—17)
式(1—17)稱為磁勢平衡程式。
變壓器帶負載工作時, 除了沿鐵心磁路而閉合的主磁通外, 還有沿空氣而閉合的漏磁通 ΦS1 、ΦS1 (圖1—4),這個磁通在初級和次級繞組中感應出漏電動勢
ES1 = -I1XS1 (1—18)
ES2 = -I2XS2 (1—19)
當電源和變壓器初級繞組構成閉合回路時,可按式(1—8)類似的方法得到
U1 = -E1+I1r1+ I1XS1 (1—20)
對于變壓器次級繞組(產生電動勢E2) 和負載構成的閉合回路中,可依據電動勢平衡定律求得
E2 = -U2-Ea2-Es2-U2+I2r2+I2XS2 (1—21)
在電阻性或電感性負載下變壓器的等效電路和矢量圖見圖1—5。 .jpg)
同樣,對中小功率變壓器,可忽略漏感搞XS1 和 XS2 ,此時
U1 = -E1+I1r1 (1—22)
E2 = -U2+I2r2 (1—23)
但是 ,當工作頻率升高時,其漏感的影響將逐漸增大 ,因此 ,音頻變壓器、高頻變壓器、脈沖變壓器必須考慮漏感的影響。
在等效電路計算中 , 往往把次級參數變換(又稱反射或歸算) 到初級,設變壓器次級負載電阻為R2 ,其值為
U2
I2
反射到初級的電阻為R2,,其值為
U1
I1
由式 (1—3) 和式(1—1)經變換后得
R2, U1 I2 E1 I2 N1 2
R2 U2 I1 E2 I1 N2
或
N1 2
N2 (1—24)
若變壓器次級為阻抗Z2 ,則反射到初級的阻抗Z2,為
N1 2
N2 (1—25)
改變(N1/N2)值,就可以改變值,這就是變壓器變換阻抗的原理。
待續...
